티스토리 뷰
https://www.acmicpc.net/problem/18223
18223번: 민준이와 마산 그리고 건우
입력의 첫 번째 줄에 정점의 개수 V와 간선의 개수 E, 그리고 건우가 위치한 정점 P가 주어진다. (2 ≤ V ≤ 5,000, 1 ≤ E ≤ 10,000, 1 ≤ P ≤ V) 두 번째 줄부터 E개의 줄에 걸쳐 각 간선의 정보
www.acmicpc.net
- 문제 :
종강을 맞은 민준이는 고향인 마산으로 내려갈 계획을 짜고 있었다. 늘 그랬듯, 마산으로 갈 버스를 예약하려던 순간 민준이는 집으로 가는 다른 방법이 떠올랐다. 그것은 직접 지도를 보고 고향으로 가는 가장 짧은 길을 찾는 것이다.
그때, 먼저 고향으로 내려갔던 친구인 건우에게 연락이 왔다. 건우는 고향으로 내려가던 중 알 수 없는 일에 휘말려 외딴곳에 혼자 남겨지게 되었다. 건우는 유일한 구세주인 민준이에게 도움을 청한 것이었다. 그러나 마산의 남자인 민준이에게는 마산이 먼저였다. 민준이는 처량한 건우를 무시한 채 고향으로 떠나려고 했지만, 만약 고향으로 가는 길에 건우가 있다면 겸사겸사 도움을 줄 수 있을 것 같았다.
지도는 양방향 그래프 형태로 되어있다. 출발지는 1번 정점 마산은 V번 정점이다. 정점은 1~V까지 있다. 건우는 P번 정점에 있다.
그리고 항상 1번 정점에서 P번과 V번 정점으로 갈 수 있는 경로가 존재한다.
중복되는 간선과 자기 자신을 가리키는 간선은 존재하지 않는다.
아래와 같은 그래프가 있을 때,
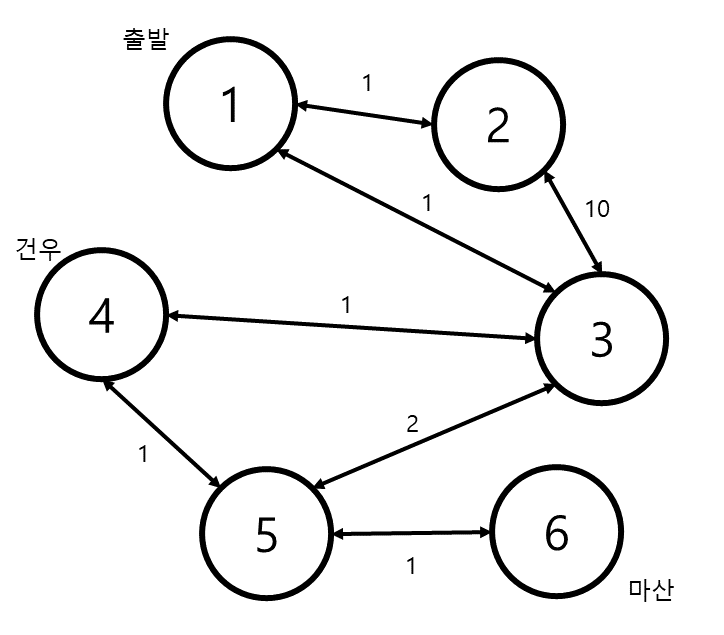
위의 경우는 최단 경로가 두 가지 있다.
1→3→4→5→6 또는 1→3→5→6 이다. 이것 중에서 건우가 있는 곳, 즉 4번 정점이 포함된 최단 경로가 있으므로 이 경우에는 민준이가 건우를 도울 수 있다.
민준이가 건우를 도와주는 경로의 길이가 최단 경로의 길이보다 길어지지 않는다면, 민준이는 반드시 건우를 도와주러 간다.
어쩌면 지킬 수도 있는 민준이의 우정을 위해 우리가 도와주자!
- 풀이 :
다익스트라로 해결할 수 있는 문제였습니다.
출발점인 1번 노드부터 V까지 가는 최단경로의 길이가 1 -> P, P -> V의 최단거리 합과 같다면 P를 거쳐서 지나가도 최단거리라는 뜻이므로 건우를 구할 수 있습니다. 같지 않은 경우 건우는 버려집니다.
- 소스코드 :
from heapq import heappush,heappop
import sys
input = sys.stdin.readline
V,E,P = map(int,input().split())
graph = [[]for _ in range(V+1)]
distance = [ float("inf") for _ in range(V+1)]
for _ in range(E):
a,b,c = map(int,input().split())
graph[a].append([b,c])
graph[b].append([a,c])
def dijkstra(start):
heap = []
heappush(heap,[0,start])
distance = [float("inf") for _ in range(V + 1)]
distance[start] = 0
while heap:
cost, curr = heappop(heap)
for next,c in graph[curr]:
totalCost = cost + c
if distance[next] > totalCost:
distance[next] = totalCost
heappush(heap,[totalCost,next])
return distance
if dijkstra(1)[V] == dijkstra(1)[P] + dijkstra(P)[V]:
print("SAVE HIM")
else:
print("GOOD BYE")'Algorithm > Dijkstra' 카테고리의 다른 글
| (Python/파이썬) - 백준(BOJ) 14284번 : 간선 이어가기 2 (0) | 2022.04.28 |
|---|---|
| (Python/파이썬) - 프로그래머스 : 배달 (0) | 2022.04.11 |
| (Python) - BOJ(2665번) : 미로만들기 (0) | 2022.03.08 |
| (Python) - BOJ(18352번) : 특정 거리의 도시 찾기 (0) | 2022.03.08 |
| (Python) - BOJ(11779번) : 최소비용 구하기 2 (0) | 2022.03.08 |



