티스토리 뷰
728x90
https://www.acmicpc.net/problem/11444
11444번: 피보나치 수 6
첫째 줄에 n이 주어진다. n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이다.
www.acmicpc.net
- 문제 :
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다.
이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가 된다.
n=17일때 까지 피보나치 수를 써보면 다음과 같다.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597
n이 주어졌을 때, n번째 피보나치 수를 구하는 프로그램을 작성하시오.
- 풀이 :
n이 엄청나게 클 때, 피보나치 수를 구하려면 행렬의 거듭제곱을 이용하면 된다.
물론 스스로 찾아낸 것은 아니고 다른 사람들의 풀이 참고 + 피보나치 수를 검색해서 나온 정보이다.
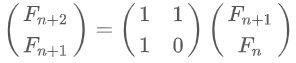
따라서, 행렬의 거듭제곱을 재귀로 구현하고 값이 너무 커지는 것을 방지하기 위해 매 재귀마다 1,000,000,007로 나누어줘야 한다.
검색해서 풀지 않았으면 절대 못 풀었을 것 같다.
참고 : https://www.acmicpc.net/blog/view/28
- 소스코드 :
p=1000000007
def power(adj,n):
if n==1:
return adj
elif n%2:
return multi(power(adj,n-1),adj)
else:
return power(multi(adj,adj),n//2)
def multi(a,b):
temp=[[0]*len(b[0]) for _ in range(2)]
for i in range(2):
for j in range(len(b[0])):
sum=0
for k in range(2):
sum+=a[i][k]*b[k][j]
temp[i][j]=sum%p
return temp
adj=[[1,1],[1,0]]
start=[[1],[1]]
n=int(input())
if n<3:
print(1)
else:
print(multi(power(adj,n-2),start)[0][0])
320x100
'Algorithm > Math' 카테고리의 다른 글
| (Python/파이썬) - 백준(BOJ) 2581번 : 소수 (0) | 2022.04.08 |
|---|---|
| (Python) - BOJ(15654번) : N과 M (5) (0) | 2022.03.03 |
| (Python) - BOJ(13258번) : 복권 + 은행 (0) | 2022.03.02 |
| (Python) - BOJ(1009번) : 분산처리 (0) | 2022.03.01 |
| (Python) - BOJ(1075번) : 나누기 (0) | 2022.02.28 |
댓글
© 2022 WonSeok, All rights reserved



